Jednadžbu oblika

\[3x+2y=5\]

nazivamo linearna jendadžba s dvije nepoznanice. Svaka dva broja koja upisana umjesto \(x\: i\: y\) u jednadžbu daju točnu jednakost su rješenje ovakve jednadžbe. Npr. očito za \(x=1\:i\:y=1\) vrijedi

\[3\cdot 1+2\cdot 1=5\]

\[5=5\]

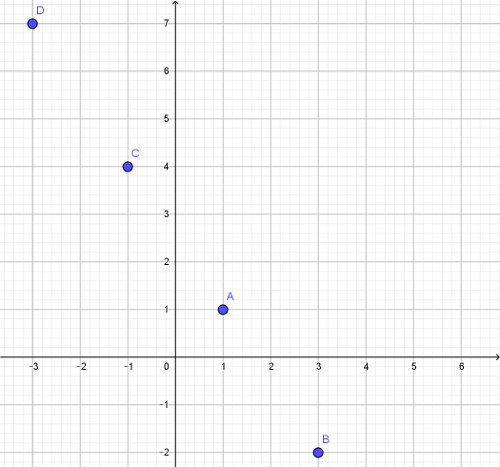
Ovo rješenje zapisujemo u obliku uređenog para \((1,1)\). Vidimo da neka rješenja možemo pogoditi, npr. uređeni parovi \((3,-2),(-1,4),(-3,7)\), itd. su rješenja početne jednadžbe (provjeri!). Slutimo da jednadžba ima beskonačno mnogo rješenja oblika \((x,y)\), jer ma koko izabrali jednu nepoznanicu \(x\:ili\:y\) uvrštenjem izabrane u jednadžbu drugu, \(y\:ili\:x\), možemo izračunati. Odredi još nekoliko rješenja, unesi ih u pravokutni koordinatni sustav i uvjeri se da točke određene uređenim parovima predstavljaju pravac u koordinatnom sustavu.

Linearnu jednadžbu kao iz navedenog primjera općenito zapisujemo u obliku

\[Ax+By=C, \:\:(A,B,C\in R)\mspace{50mu}(5.1)\]

Realne brojeve \(A,B\:i\:C\) nazivamo koeficijentima linearne jednadžbe i pri čemu je bar jedan od koeficijenata \(A,B\) različit od nule. Graf linearne funkcije je pravac. Za linearnu jednadžbu \((5.1)\) kažemo da je implicitni oblik jednadžbe pravca.