Kojom je formulom zadana kvadratna funkcija čiji je graf prikazan na slici? 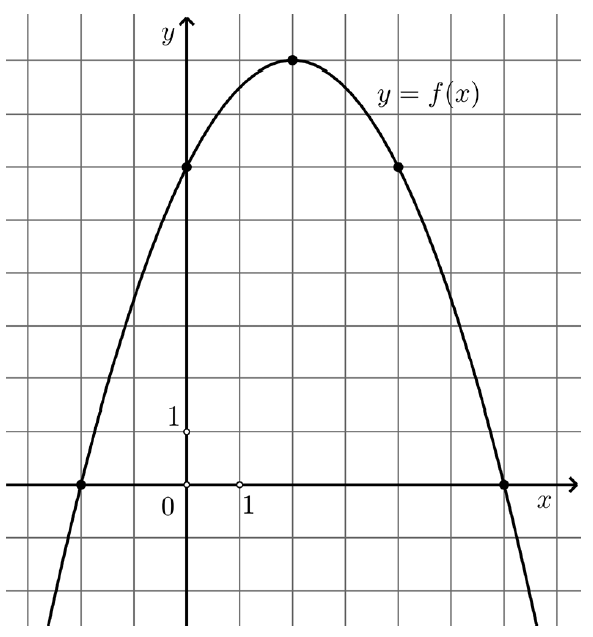
| A. | \(f(x)=-\frac 12 x^2+2x+6\) | |
| B. | \(f(x)=-\frac 12 x^2-2x-6\) | |
| C. | \(f(x)=-x^2-2x+6\) | |
| D. | \(f(x)=-x^2+2x-6\) |
Napomena: drugi razred.
\(\textbf{Rješenje: }\)Točke grafa funkcije u redom:
- Presjek s \( y-osi \) je točka \( (0,6) \) što znači da je slobodni koeficijent \( c=6 \)
- nulltočke su \( (-2,0) \) i \( (6,0) \)
- tjeme je točka \( (2,8) \) i
- još jedna vidiljiva iz grafa \( (4,6) \)
Slobodan koeficijent \( c=6 \) imaju samo funkcije pod A i C. Treba provjeriti s još bar jednom točkom. Najjednostavnije je uzeti neku od nulltočaka, npr za \( (-2,0) \) je u prvoj funkciji \[-\frac12\cdot(-2)^2+2\cdot (-2)+6= -2-4+6=0 \] i to je naša funkcija.
Odgovor je - \(\textbf{A.}\: \color{red}{\heartsuit}\)
