B)Prikazan je kvadrat ABCD podijeljen na 9 sukladnih manjih kvadrata. Koliko je posto površine kvadrata ABCD osjenčano?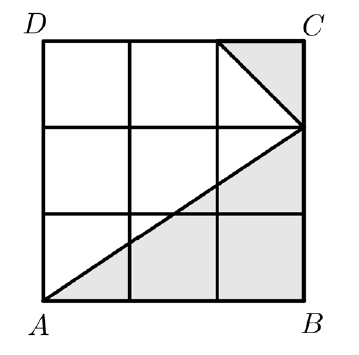
| A. | 33.33 | B. | 38.89 | C. | 44.44 | D. | 46.47 |
Napomena: drugi razred.
\(\color{green}{\textbf{Rješenje: }}\)
Radi se o procentnom računu. Kao mjeru uzmimo manji kvadrat. Tada je površina cijelog lika \( P= 3\cdot 3=9 \) manjih kvadrata. Osjenčeni dio čine dva pravokutna trokuta. Prvi je gornji desni koji ima površinu \( P_1=\frac 12 \) manjeg kvadrata a drugi osjenčeni dio je pravokutni trokut starnica \( 3 \) i \( 2 \) površine \( P_2=\frac{3\cdot 2}2=3 \). Osjenčena površima je \( 3+\frac 12=\frac 72 \).
Postavimo razmjer
\begin{gather*}
P:100=(P_1+P_2):x\\
9:100=\frac 72 :x\\
x=\frac{100\cdot\frac 72}{9}\\
x=38.8888888888\ldots
\end{gather*}
Zaokruženo na dvije decimale je \( x=38.89 \).
Točan odgovor je pod \(\textbf{B.} \color{red}{\heartsuit}\)
