Detalji
Hitova: 1267
 1. Eksplocitni oblik jednadžv pravca

\[y=ax+b\left(a,b\in R\right)\qquad\qquad{(1)}\]

  • a - koeficijent smjera pravca (nagib pravca)
  • b - odrezak na \(y-osi\)
2. Implicitni oblik jednadžv pravca

\[Ax+By+C=0;\left(A,B,C\in R\right)\qquad\qquad{(2)}\]

Detalji
Hitova: 2884

Ako su u jednadžb1 (5.1) koeficijenti \(A\neq 0,B\neq 0\:i\:C=0\) jednažba je oblika

\[Ax+By=0\].

Detalji
Hitova: 2353

Jednadžbu oblika

\[3x+2y=5\]

nazivamo linearna jendadžba s dvije nepoznanice. Svaka dva broja koja upisana umjesto \(x\: i\: y\) u jednadžbu daju točnu jednakost su rješenje ovakve jednadžbe. Npr. očito za \(x=1\:i\:y=1\) vrijedi

\[3\cdot 1+2\cdot 1=5\]

\[5=5\]

Detalji
Hitova: 1894

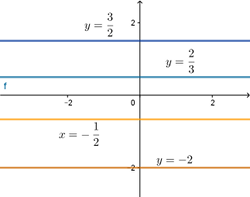
Ako u jednadžbi \((5.1)\) za koeficijente vrijedi \(A=0, B\neq 0\)  jednadžba ima oblik 

\[By+C=0\]

Rješenje je \(y=-\frac{C}{b}\), i uvodeći oznaku \(-\frac{C}{b}=y_1\) imamo jednadžbu \(\mathbf{y=y_1}\). Ovom jednadžbom date su točke ravnine s ordinatom \(y_1\) dok apscisa može biti bilo koji realan broj. Te točke leže na pravcu koji prolazi točkom \((0,y_1)\) i paralelan s \(x-osi\)..