Pravac

Već znamo da linearna jednadžba oblika \(Ax+By+C=0\) ima beskonačno mnogo rješenja i da ih zapisujemo u obliku uređenih parpva  \((x,y)\) realnihbrojeva. Ta rješenja u koordinatnom sustavu predstavljaju pravac.

\(\text{Definicija 1.}\:\)Pravac  je skup svih točaka \(( x,y)\) u ravnini čije koordinate zadovoljavaju jednadžbu

\[Ax+By+C=0, \:\:(A,B,C\in R)\mspace{50mu}(8.1)\]

pri čemu je bar jedan od koeficijenata \(A,B\) različit od nule. Ova se jednadžba naziva \(\textbf{implicitni oblik jednadžbe pravca.}\)

    Posebni oblici    

U ovisnosti o koeficijentima jednadžbe (8.1) mogući su:

 \(\mathbf{I)\:\:A\neq0,\: B\neq 0,\:C=0}\)    

Jednažba je oblika \[Ax+By=0\]. Za \(x=0\:ili\:y=0\) kao rješenje imamo \((0,0)\) što znači da svi ovakvi pravci prolaze ishodištem koordinatnog sustava.

   \(\mathbf{II)\:\:A=0, B\neq 0}\)    

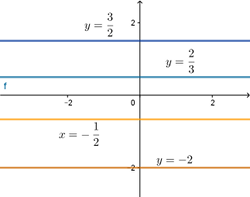Jednadžba ima oblik 

\[By+C=0\]

Rješenje je \(y=-\frac{C}{B}\), i uvodeći oznaku \(-\frac{C}{B}=y_1\) imamo jednadžbu \(\mathbf{y=y_1}\). Ova jednadžba određuje točke ravnine s ordinatom \(y_1\) dok apscisa može biti bilo koji realni brojje. Takve točke leže na pravcu koji prolazi točkom \((0,y_1)\) i paralelan je s \(x-osi\).

\(\mathbf{III)\:\:A\neq 0, B= 0}\)   

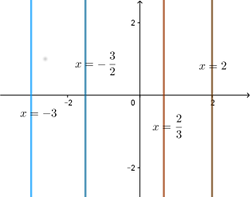Jednadžba ima oblik 

\[Ax+C=0\]

Rješenje je \(x=-\frac{C}{A}\), i uvodeći oznaku \(-\frac{C}{A}=x_1\) imamo jednadžbu \(\mathbf{x=x_1}\). Ovom jednadžbom date su točke ravnine s apscisom \(x_1\) dok ordinata može biti bilo koji realan broj. Te točke ležena pravcu koji prolazi točkom \((x_1,0)\) i paralelan s \(y-osi\)..