Vektori koji imaju isti pravac nositelj jednaki su ako imaju istu duljinu i orjentaciju.
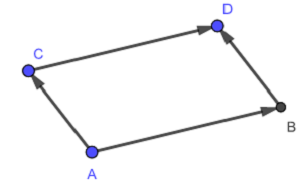
\(\mathbf{Tvrdnja\:1.}\:\) ( kriterij jednakosti vektora) Vektori \(\overrightarrow{AB}\) i \(\overrightarrow{CD}\) su jednaki ako i samo ako je četverokut \(ABDC\) paralelogram.

\(\mathbf{Definicija\:4.}\:\) Neka je \(O\) Istaknuta točka ravnine, a \(T\) bilo koja proizvoljna točka te ravnine. Vektor \(\overrightarrow{OT}\) nazivamo \(\textbf{radij vektor}\) točke \(T\).

\(\mathbf{Tvrdnja\:2.}\:\) Neka je \(O\) bilo koja odabrana točka ravnine i \(\overrightarrow{AB}\) zadani vektor. Tada postoji jednisrvena točka \(T\) u ravnini za koju je \(\overrightarrow{OT}=\overrightarrow{AB}.\)

Za svaki vektor možemo odrediti njemu jednak, a koji ima početak u u naprijed izabranoj točki \(O\). Kažemo da hvatište vektora možemo izabrati povolji.